O físico Geoffrey West descobriu que simples leis matemáticas governam as propriedades das cidades. Coisas como riqueza, a criminalidade, a ...
O físico Geoffrey West descobriu que simples leis matemáticas governam as propriedades das cidades. Coisas como riqueza, a criminalidade, a mobilidade entre outros aspectos podem ser deduzidos a partir de um único número: sua população. Nesta palestra alucinante no TEDGlobal ele mostra como isso funciona e como leis similares podem ser aplicadas a organismos e corporações.
As cidades são o crisol da civilização. Elas vêm se expandindo, a urbanização está se expandindo, a uma taxa exponencial nos últimos 200 anos, de tal modo que na metade deste século, o planeta estará completamente dominado por cidades.
As cidades são a origem do aquecimento global, do impacto no meio ambiente, saúde, poluição, doenças, finanças, economias, energia -- são todos problemas com os quais nos confrontamos por existirem as cidades. É de onde vêm estes problemas todos. E o tsunami de problemas que estamos enfrentando em relação às questões de sustentabilidade, são na verdade um reflexo do crescimento exponencial da urbanização por todo o planeta.
Tenho aqui alguns números. Há 200 anos, os Estados Unidos tinham menos de 4% de urbanização. Agora esse número chega a mais de 82%. O planeta ultrapassou a marca de 50% alguns anos atrás. A China vai construir 300 novas cidades nos próximos 20 anos. Agora ouçam isto: Toda semana num futuro previsível, até 2050, toda semana mais de um milhão de pessoas somam-se às nossas cidades.
Isto vai afetar tudo. Todas as pessoas nesta sala, se estiverem vivas, serão afetadas pelo que está acontecendo nas cidades neste extraordinário fenômeno. Contudo, as cidades, apesar de terem este aspecto negativo associado a elas, também são a solução. Porque as cidades são os aspiradores e os imãs que têm atraído as pessoas criativas, criando idéias, inovando, gerando riquezas, etc... Temos esta espécie de dualidade natural. E há uma necessidade urgente de desenvolver uma teoria científica das cidades.
Estes são os meus companheiros de luta. Este trabalho tem sido feito com um grupo extraordinário de pessoas, eles fazem todo o trabalho, e eu sou o que conta as besteiras e tenta juntar isso tudo.
(Risos)
E aqui está o problema: isto é o que todos queremos. Os 10 bilhões de pessoas no planeta em 2050 querem viver em lugares como este...
ter coisas como estas...
fazer coisas como estas...
com economias que crescem assim,
não percebendo que a entropia produz coisas como isto...
isto...
isto...
e isto.
E a questão é: É assim que Edimburgo, Londres e Nova York serão em 2050...
ou então serão assim?
Esta é a questão. Devo dizer que, muitos dos indicadores mostram que será assim, mas falemos sobre isto.
Então, a minha provocadora afirmação é que nós precisamos desesperadamente de uma teoria científica séria das cidades. E por teoria científica quero dizer quantificável - baseada em princípios genéricos subjacentes que pode ser realizada num quadro preditivo. É o que busco. É concebível? Haverá leis universais? Há duas questões que me vêm à cabeça quando penso neste problema. A primeira é: As cidades são parte da Biologia? Será Londres uma baleia enorme? Será Edimburgo um cavalo? Será a Microsoft um grande formigueiro? O que aprendemos com isto?
Nós as usamos metaforicamente - o DNA de uma companhia, o metabolismo de uma cidade, e daí por diante - são apenas besteiras, besteiras metafóricas, ou há algum argumento sério nisso? E se é o caso, por que é tão difícil matar uma cidade? Vocês poderiam jogar uma bomba atômica numa cidade, e 30 anos depois ela estaria sobrevivendo. Muito poucas cidades desaparecem.
Então isso...
é apenas uma outra versão disto?
Nós compreendemos isto muito bem. Perguntem qualquer questão genérica sobre isto -- quantas árvores de um determinado tamanho, quantos ramos de um determinado tamanho tem uma árvore, quantas folhas, qual é a energia que flui em cada ramo, qual é o tamanho da copa, qual é seu crescimento, qual é sua mortalidade? Nós temos um quadro matemático baseado em princípios genéricos universais que pode responder estas questões. E a ideia é, podemos fazer o mesmo em relação a isto? Então, o caminho é reconhecer que uma das coisas mais extraordinárias sobre a vida, é a possibilidade de sua representação em escala, e isso funciona em uma amplitude extraordinária. Este é um pequeno exemplo dessa amplitude, na verdade; Somos nós, os mamíferos, somos um destes.
Os mesmos princípios, as mesmas dinâmicas, a mesma organização funciona em tudo isto, incluindo nós mesmos, e pode estar em escalas, representando proporções de até 100 milhões. E este é um dos principais motivos da vida ser tão resiliente e robusta - "escalabilidade". Vamos discutir isso daqui a pouco.
Vocês sabem, a um nível local, todos nesta sala são representados em escala. Isso é chamado de crescimento. Vejam como vocês crescem.
Um rato, isto é um rato - poderia ser um de vocês.
Nós somos muito parecidos. E como veem, vocês são familiarizados com isto. Crescemos muito rápido e depois paramos.
E aquela linha ali é uma previsão da mesma teoria, baseada nos mesmos princípios, que descrevem aquela floresta. E este aqui é o crescimento de um rato. E aqueles pontos lá são dados. Isto é apenas o peso em função da idade. E como podem ver, ele para de crescer. Muito, muito bom para a biologia -- e também uma das razões para a sua grande resiliência. Muito, muito ruim para a economia, empresas e cidades em nosso paradigma atual. É no que acreditamos. Isto é o que toda a economia está nos impondo, particularmente ilustrada nesse canto esquerdo: bastões de hockey. Esta é uma série de empresas de software -- e esses são seus rendimentos em função da idade -- todos crescendo bastante, e todo mundo ganhando milhões e bilhões de dólares.
Ok, como é que entendemos isto? Por isso, primeiro vamos falar de biologia. Isto explicitamente nos mostra como as coisas são representadas em escala. E este é um gráfico verdadeiramente notável.
O que está aqui traçado é a taxa metabólica - quanta energia é necessária por dia para nos mantermos vivos - em função do peso, da massa, para nossos organismos. E foi traçada neste jeito curioso, crescente, por fatores de 10, de outra maneira não seria possível colocar tudo no gráfico. E o que podemos ver se você traçá-lo desta forma um pouco curiosa, é que todo mundo está na mesma linha. Apesar do fato deste ser o sistema mais complexo e diverso do universo, há uma simplicidade extraordinária expressa aqui. É particularmente surpreendente porque cada um destes organismos, cada subsistema, cada tipo de célula, cada gene, evoluiu em seu próprio e único nicho ambiental com sua própria história. E ainda assim, apesar de toda a evolução darwinista e seleção natural, eles têm sido forçados a permanecer numa linha.
Alguma coisa está acontecendo. Antes de falar sobre isso, eu escrevi ali embaixo a inclinação desta curva, esta linha reta. São ¾, a grosso modo, que é menos de 1 - e nós a chamamos de sublinear. E este é o ponto da questão. Diz que, se fosse linear, a inclinação mais acentuada, então, duplicando o tamanho você precisaria do dobro da quantidade de energia. Mas é sublinear, e significa que, se duplicarmos o tamanho do organismo, na verdade só precisaremos de mais 75% de energia. E por isso algo maravilhoso na biologia é que expressa uma extraordinária economia de escala. Sistematicamente quanto maior você for, de acordo com regras muito bem definidas, menos energia per capita. Agora qualquer variável fisiológica em que possam pensar, qualquer história de vida em que possam pensar, se for traçada desta maneira, fica assim. Há uma regularidade extraordinária. Digam-me o tamanho de um mamífero, eu posso dizer a vocês com 90% de certeza tudo sobre ele em termos de fisiologia, história de vida, etc...
E isto se deve às redes. Tudo na vida é controlado por redes -- desde o intracelular ao multicelular em nível do ecossistema. E vocês conhecem bem estas redes.
Isso é uma pequena coisa que vive dentro de um elefante. E aqui está o resumo do que estou dizendo. Se pegarem essas redes, esta ideia de redes, e aplicarem princípios universais, princípios matemáticos, universais, todas estas representações em escalas e todas estas restrições se sucedem, incluindo a descrição da floresta, a descrição de nosso sistema circulatório, a descrição do interior das células. Uma das coisas que eu não mencionei na introdução foi que, sistematicamente, o ritmo de vida diminui à medida em que você cresce. O ritmo cardíaco é mais lento, você vive mais; a difusão de oxigênio e os recursos dentro das membranas é menor, etc.
A questão é: algo disto é verdadeiro para as cidades e empresas? Então, Londres é uma Birmingham em maior escala, que por sua vez é uma Brighton em maior escala, etc., etc.? Seria Nova York uma São Francisco em maior escala, que é uma Santa Fé em maior escala? Não sabemos. Nós vamos discutir isso. Mas elas são redes. E o mais importante na rede das cidades são vocês.
As cidades são uma manifestação física das suas interações, das nossas interações, e da agregação e agrupamento de indivíduos. Aqui está uma fotografia simbólica disso. E aqui estão escalas de cidades. Isto mostra que neste exemplo simples, que por acaso é um exemplo banal do número de postos de gasolina em função do tamanho - traçado da mesma maneira que na biologia - vocês podem ver exatamente o mesmo tipo de coisa.
Há uma evolução na escala. O número de postos de gasolina na cidade agora é dado a vocês quando me dizem o tamanho dela. A inclinação disso é menos que linear. Há uma economia de escala. Menos postos de gasolina per capita quanto maior você for - não é surpreendente. Mas aqui está o que é surpreendente. O resultado da escala é igual em todo lugar. Aqui estão apenas países europeus, mas se fizermos no Japão, China ou Colômbia, é sempre o mesmo com o mesmo tipo de economia de escala no mesmo grau. E qualquer infraestrutura que observamos -- seja o comprimento de estradas, o comprimento das linhas elétricas -- qualquer coisa que você vê tem a mesma economia de escala, da mesma maneira. É um sistema integrado que evoluiu apesar de todo o planejamento e todo o resto. Mas ainda mais surpreendente é que se observarmos as 'quantidades' socioeconômicas, quantidades que não têm analogia na biologia, que evoluíram quando começamos a formar comunidades 8 a 10.000 anos atrás.
A de cima é o salário em função do tamanho representado da mesma maneira. E a de baixo representa vocês - super criativos representados da mesma maneira. E o que podem ver é um fenômeno de escala. Mas o mais importante nisto, o expoente, o análogo a esses ¾ para a taxa metabólica, é maior do que um - é cerca de 1.15 a 1.2. Aqui está, diz que quanto maior você for mais terá per capita, contrariamente à biologia - maiores salários, mais pessoas criativas per capita à medida que somos maiores, mais patentes per capita, mais crime per capita.
E nós olhamos tudo: casos de HIV, gripe, etc. E aqui, estão todos representados em conjunto.
Só para mostrar a vocês como representamos, aqui está a renda, PIB -- PIB da cidade -- crime e patentes todos num só gráfico. E podem ver, todos seguem a mesma linha. E aqui está a afirmação.
Qual é a razão disto? Eu não tenho tempo para mostrar a vocês toda a matemática, mas por trás disto estão as redes sociais, porque este é um fenômeno universal.
Japão, Chile, Portugal, Escócia, não interessa. Sempre, todos os dados mostram que é igual, apesar destas cidades terem evoluído independentemente. Algo universal está acontecendo. A universalidade, repito, somos nós -- nós somos a cidade. E são as nossas interações e o agrupamento dessas interações. E aqui está, como já disse. Então se são essas redes e suas estruturas matemáticas, contrariamente à biologia, de escala sublinear, economias de escala, você teria a diminuição do ritmo de vida à medida que crescemos. Se são redes sociais com escalas super-lineares -- mais per capita -- então a teoria diz que você aumenta o ritmo de vida. Quanto maior você for, mais rápida ficará a vida. À esquerda está a frequência cardíaca que a biologia mostra. À direita está a velocidade do passo numa série de países europeus, mostrando esse aumento.
Por último, quero falar sobre crescimento. Isto é o que temos na biologia, repito. Economias de escala deram origem a este comportamento sigmoidal. Crescemos rápido e depois paramos - parte da nossa resiliência. Isso seria ruim para as economias e cidades. E na verdade, uma das coisas extraordinárias da teoria é que se temos escalas super-lineares a partir da criação de riquezas e inovação, então na verdade temos, segundo a mesma teoria, um belo crescimento exponencial da curva - adorável. E na verdade, se a compararem com os dados, ela se encaixa muito bem com o desenvolvimento das cidades e das economias.
Mas há um problema terrível. E o problema é que este sistema está destinado ao colapso. E está destinado ao colapso por várias razões -- razões de tipo "malthusiano" -- de que esgotamos os recursos. E como se evita isso? Bem, já o fizemos antes.
O que fazemos é, à medida que crescemos e nos aproximamos do colapso, uma inovação maior entra em cena e começamos tudo novamente.
E começamos de novo quando nos aproximamos do próximo, e daí por diante. Por isso há ciclos contínuos de inovação que são necessários para sustentar o crescimento e evitar o colapso.
Contudo, o problema é que temos de inovar cada vez mais rápido. Por isso a imagem é que não estamos apenas em uma esteira que vai mais rápido, mas temos que mudar a esteira mais e mais rápido. Temos de acelerar continuamente. E a questão é: podemos, enquanto seres socioeconômicos evitar um ataque de coração?
E finalmente, vou terminar nestes últimos minutos perguntando sobre as empresas. Vejam as empresas, elas evoluem em escala. A primeira é, de fato, Walmart à direita. É o mesmo gráfico. Estes são os rendimentos e os ativos em função do tamanho da empresa conforme o número de seus empregados. Poderíamos usar vendas, o que quiserem. Aqui está: após algumas flutuações no início, quando as empresas estão inovando elas crescem lindamente. E nós olhamos 23.000 empresas, nos Estados Unidos, devo dizer. E estou mostrando a vocês apenas um pouco disto.
O que é surpreendente sobre as empresas é que seguem na escala sublinearmente como a biologia, indicando que elas são dominadas, não por super-lineares inovação e ideias; elas tornam-se dominadas pelas economias de escala.
Nessa interpretação, pela burocracia e administração, e elas fazem isso lindamente, devo dizer. Por isso se me disserem o tamanho de uma empresa, alguma empresa pequena, eu poderia ter previsto o tamanho da Walmart. Se tivesse esta escala sublinear, a teoria diz que deveríamos ter crescimento sigmoidal. Ali está a Walmart. Não parece muito sigmoidal. É disto que gostamos, bastões de hockey Mas se vocês repararem, eu trapaceei, porque eu apenas fui até 1994. Vamos até 2008.
Essa linha vermelha vem da teoria. Então, se eu tivesse feito isto em 1994, poderia ter previsto o que o Walmart seria agora. E isto se repete em todo o espectro de empresas. Ali estão. São 23.000 empresas.
Elas começam todas parecendo bastões de hockey, todas se inclinam, e todas morrem como vocês e eu.
Obrigado.
(Aplausos)
[Via BBA]
As cidades são o crisol da civilização. Elas vêm se expandindo, a urbanização está se expandindo, a uma taxa exponencial nos últimos 200 anos, de tal modo que na metade deste século, o planeta estará completamente dominado por cidades.
As cidades são a origem do aquecimento global, do impacto no meio ambiente, saúde, poluição, doenças, finanças, economias, energia -- são todos problemas com os quais nos confrontamos por existirem as cidades. É de onde vêm estes problemas todos. E o tsunami de problemas que estamos enfrentando em relação às questões de sustentabilidade, são na verdade um reflexo do crescimento exponencial da urbanização por todo o planeta.
Tenho aqui alguns números. Há 200 anos, os Estados Unidos tinham menos de 4% de urbanização. Agora esse número chega a mais de 82%. O planeta ultrapassou a marca de 50% alguns anos atrás. A China vai construir 300 novas cidades nos próximos 20 anos. Agora ouçam isto: Toda semana num futuro previsível, até 2050, toda semana mais de um milhão de pessoas somam-se às nossas cidades.
 |
| Toda semana num futuro previsível, até 2050, mais de um milhão de pessoas somam-se às nossas cidades. |
Estes são os meus companheiros de luta. Este trabalho tem sido feito com um grupo extraordinário de pessoas, eles fazem todo o trabalho, e eu sou o que conta as besteiras e tenta juntar isso tudo.
(Risos)
E aqui está o problema: isto é o que todos queremos. Os 10 bilhões de pessoas no planeta em 2050 querem viver em lugares como este...
ter coisas como estas...
fazer coisas como estas...
com economias que crescem assim,
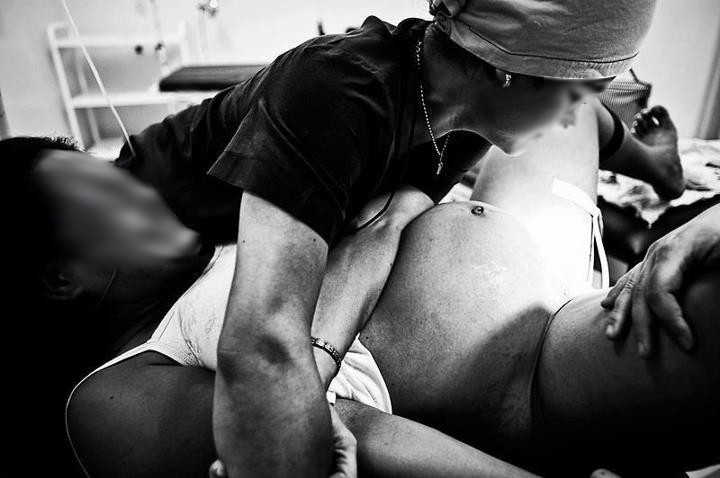
não percebendo que a entropia produz coisas como isto...
isto...
isto...
 |
| "Aumento maciço de inquéritos sobre os crimes com faca" |
E a questão é: É assim que Edimburgo, Londres e Nova York serão em 2050...
ou então serão assim?
Esta é a questão. Devo dizer que, muitos dos indicadores mostram que será assim, mas falemos sobre isto.
Então, a minha provocadora afirmação é que nós precisamos desesperadamente de uma teoria científica séria das cidades. E por teoria científica quero dizer quantificável - baseada em princípios genéricos subjacentes que pode ser realizada num quadro preditivo. É o que busco. É concebível? Haverá leis universais? Há duas questões que me vêm à cabeça quando penso neste problema. A primeira é: As cidades são parte da Biologia? Será Londres uma baleia enorme? Será Edimburgo um cavalo? Será a Microsoft um grande formigueiro? O que aprendemos com isto?
| "Serão as cidades apenas organismos muito grandes satisfazendo as leis da biologia?" "Por que todas as empresas falem enquanto quase todas as cidades sobrevivem?" |
Todas as empresas morrem, todas as empresas. E se vocês têm uma teoria séria, vocês devem ser capazes de predizer quando a Google vai falir.
Então isso...
é apenas uma outra versão disto?
Nós compreendemos isto muito bem. Perguntem qualquer questão genérica sobre isto -- quantas árvores de um determinado tamanho, quantos ramos de um determinado tamanho tem uma árvore, quantas folhas, qual é a energia que flui em cada ramo, qual é o tamanho da copa, qual é seu crescimento, qual é sua mortalidade? Nós temos um quadro matemático baseado em princípios genéricos universais que pode responder estas questões. E a ideia é, podemos fazer o mesmo em relação a isto? Então, o caminho é reconhecer que uma das coisas mais extraordinárias sobre a vida, é a possibilidade de sua representação em escala, e isso funciona em uma amplitude extraordinária. Este é um pequeno exemplo dessa amplitude, na verdade; Somos nós, os mamíferos, somos um destes.
Os mesmos princípios, as mesmas dinâmicas, a mesma organização funciona em tudo isto, incluindo nós mesmos, e pode estar em escalas, representando proporções de até 100 milhões. E este é um dos principais motivos da vida ser tão resiliente e robusta - "escalabilidade". Vamos discutir isso daqui a pouco.
 |
| "Escalabilidade" |
 |
| Mamíferos variam em tamanho por 8 ordens de magnitude. |
Nós somos muito parecidos. E como veem, vocês são familiarizados com isto. Crescemos muito rápido e depois paramos.
 |
| Gráfico do crescimento do rato Peso (g) X Idade (em dias) |
 |
| Clique na imagem para ampliar. |
 |
| Taxa metabólica (em Watt) X Massa corpórea (em quilos) |
Alguma coisa está acontecendo. Antes de falar sobre isso, eu escrevi ali embaixo a inclinação desta curva, esta linha reta. São ¾, a grosso modo, que é menos de 1 - e nós a chamamos de sublinear. E este é o ponto da questão. Diz que, se fosse linear, a inclinação mais acentuada, então, duplicando o tamanho você precisaria do dobro da quantidade de energia. Mas é sublinear, e significa que, se duplicarmos o tamanho do organismo, na verdade só precisaremos de mais 75% de energia. E por isso algo maravilhoso na biologia é que expressa uma extraordinária economia de escala. Sistematicamente quanto maior você for, de acordo com regras muito bem definidas, menos energia per capita. Agora qualquer variável fisiológica em que possam pensar, qualquer história de vida em que possam pensar, se for traçada desta maneira, fica assim. Há uma regularidade extraordinária. Digam-me o tamanho de um mamífero, eu posso dizer a vocês com 90% de certeza tudo sobre ele em termos de fisiologia, história de vida, etc...
 |
| Quanto maior você, menos você necessita per "capita". |
E isto se deve às redes. Tudo na vida é controlado por redes -- desde o intracelular ao multicelular em nível do ecossistema. E vocês conhecem bem estas redes.
Isso é uma pequena coisa que vive dentro de um elefante. E aqui está o resumo do que estou dizendo. Se pegarem essas redes, esta ideia de redes, e aplicarem princípios universais, princípios matemáticos, universais, todas estas representações em escalas e todas estas restrições se sucedem, incluindo a descrição da floresta, a descrição de nosso sistema circulatório, a descrição do interior das células. Uma das coisas que eu não mencionei na introdução foi que, sistematicamente, o ritmo de vida diminui à medida em que você cresce. O ritmo cardíaco é mais lento, você vive mais; a difusão de oxigênio e os recursos dentro das membranas é menor, etc.
A questão é: algo disto é verdadeiro para as cidades e empresas? Então, Londres é uma Birmingham em maior escala, que por sua vez é uma Brighton em maior escala, etc., etc.? Seria Nova York uma São Francisco em maior escala, que é uma Santa Fé em maior escala? Não sabemos. Nós vamos discutir isso. Mas elas são redes. E o mais importante na rede das cidades são vocês.
As cidades são uma manifestação física das suas interações, das nossas interações, e da agregação e agrupamento de indivíduos. Aqui está uma fotografia simbólica disso. E aqui estão escalas de cidades. Isto mostra que neste exemplo simples, que por acaso é um exemplo banal do número de postos de gasolina em função do tamanho - traçado da mesma maneira que na biologia - vocês podem ver exatamente o mesmo tipo de coisa.
Há uma evolução na escala. O número de postos de gasolina na cidade agora é dado a vocês quando me dizem o tamanho dela. A inclinação disso é menos que linear. Há uma economia de escala. Menos postos de gasolina per capita quanto maior você for - não é surpreendente. Mas aqui está o que é surpreendente. O resultado da escala é igual em todo lugar. Aqui estão apenas países europeus, mas se fizermos no Japão, China ou Colômbia, é sempre o mesmo com o mesmo tipo de economia de escala no mesmo grau. E qualquer infraestrutura que observamos -- seja o comprimento de estradas, o comprimento das linhas elétricas -- qualquer coisa que você vê tem a mesma economia de escala, da mesma maneira. É um sistema integrado que evoluiu apesar de todo o planejamento e todo o resto. Mas ainda mais surpreendente é que se observarmos as 'quantidades' socioeconômicas, quantidades que não têm analogia na biologia, que evoluíram quando começamos a formar comunidades 8 a 10.000 anos atrás.
A de cima é o salário em função do tamanho representado da mesma maneira. E a de baixo representa vocês - super criativos representados da mesma maneira. E o que podem ver é um fenômeno de escala. Mas o mais importante nisto, o expoente, o análogo a esses ¾ para a taxa metabólica, é maior do que um - é cerca de 1.15 a 1.2. Aqui está, diz que quanto maior você for mais terá per capita, contrariamente à biologia - maiores salários, mais pessoas criativas per capita à medida que somos maiores, mais patentes per capita, mais crime per capita.
E nós olhamos tudo: casos de HIV, gripe, etc. E aqui, estão todos representados em conjunto.
Só para mostrar a vocês como representamos, aqui está a renda, PIB -- PIB da cidade -- crime e patentes todos num só gráfico. E podem ver, todos seguem a mesma linha. E aqui está a afirmação.
Aumenta cerca de 15%. E temos 15% de economia na infraestrutura. Esta, sem dúvida, é a razão de um milhão de pessoas por semana se juntarem às cidades. Porque pensam que todas essas coisas maravilhosas, como pessoas criativas, saúde, salários, são o que as atrai, esquecendo o feio e o mau.Se duplicarem o tamanho de uma cidade de 100.000 para 200.000, de um milhão para dois milhões, de 10 para 20 milhões, não faz diferença, porque sistematicamente há um aumento de 15% nos salários, saúde, número de casos de HIV, número de policiais, em tudo que possam pensar.
Qual é a razão disto? Eu não tenho tempo para mostrar a vocês toda a matemática, mas por trás disto estão as redes sociais, porque este é um fenômeno universal.
Esta regra dos 15% é verdadeira onde quer que você esteja no planeta.
Japão, Chile, Portugal, Escócia, não interessa. Sempre, todos os dados mostram que é igual, apesar destas cidades terem evoluído independentemente. Algo universal está acontecendo. A universalidade, repito, somos nós -- nós somos a cidade. E são as nossas interações e o agrupamento dessas interações. E aqui está, como já disse. Então se são essas redes e suas estruturas matemáticas, contrariamente à biologia, de escala sublinear, economias de escala, você teria a diminuição do ritmo de vida à medida que crescemos. Se são redes sociais com escalas super-lineares -- mais per capita -- então a teoria diz que você aumenta o ritmo de vida. Quanto maior você for, mais rápida ficará a vida. À esquerda está a frequência cardíaca que a biologia mostra. À direita está a velocidade do passo numa série de países europeus, mostrando esse aumento.
Por último, quero falar sobre crescimento. Isto é o que temos na biologia, repito. Economias de escala deram origem a este comportamento sigmoidal. Crescemos rápido e depois paramos - parte da nossa resiliência. Isso seria ruim para as economias e cidades. E na verdade, uma das coisas extraordinárias da teoria é que se temos escalas super-lineares a partir da criação de riquezas e inovação, então na verdade temos, segundo a mesma teoria, um belo crescimento exponencial da curva - adorável. E na verdade, se a compararem com os dados, ela se encaixa muito bem com o desenvolvimento das cidades e das economias.
Mas há um problema terrível. E o problema é que este sistema está destinado ao colapso. E está destinado ao colapso por várias razões -- razões de tipo "malthusiano" -- de que esgotamos os recursos. E como se evita isso? Bem, já o fizemos antes.
O que fazemos é, à medida que crescemos e nos aproximamos do colapso, uma inovação maior entra em cena e começamos tudo novamente.
E começamos de novo quando nos aproximamos do próximo, e daí por diante. Por isso há ciclos contínuos de inovação que são necessários para sustentar o crescimento e evitar o colapso.
Contudo, o problema é que temos de inovar cada vez mais rápido. Por isso a imagem é que não estamos apenas em uma esteira que vai mais rápido, mas temos que mudar a esteira mais e mais rápido. Temos de acelerar continuamente. E a questão é: podemos, enquanto seres socioeconômicos evitar um ataque de coração?
E finalmente, vou terminar nestes últimos minutos perguntando sobre as empresas. Vejam as empresas, elas evoluem em escala. A primeira é, de fato, Walmart à direita. É o mesmo gráfico. Estes são os rendimentos e os ativos em função do tamanho da empresa conforme o número de seus empregados. Poderíamos usar vendas, o que quiserem. Aqui está: após algumas flutuações no início, quando as empresas estão inovando elas crescem lindamente. E nós olhamos 23.000 empresas, nos Estados Unidos, devo dizer. E estou mostrando a vocês apenas um pouco disto.
O que é surpreendente sobre as empresas é que seguem na escala sublinearmente como a biologia, indicando que elas são dominadas, não por super-lineares inovação e ideias; elas tornam-se dominadas pelas economias de escala.
Nessa interpretação, pela burocracia e administração, e elas fazem isso lindamente, devo dizer. Por isso se me disserem o tamanho de uma empresa, alguma empresa pequena, eu poderia ter previsto o tamanho da Walmart. Se tivesse esta escala sublinear, a teoria diz que deveríamos ter crescimento sigmoidal. Ali está a Walmart. Não parece muito sigmoidal. É disto que gostamos, bastões de hockey Mas se vocês repararem, eu trapaceei, porque eu apenas fui até 1994. Vamos até 2008.
Essa linha vermelha vem da teoria. Então, se eu tivesse feito isto em 1994, poderia ter previsto o que o Walmart seria agora. E isto se repete em todo o espectro de empresas. Ali estão. São 23.000 empresas.
Elas começam todas parecendo bastões de hockey, todas se inclinam, e todas morrem como vocês e eu.
Obrigado.
(Aplausos)
[Via BBA]